What is Dispersive Flies Optimisation, and where can we use it?

DFO is a swarm intelligence based ‘meta-heuristic’ (problem independent computational method), similar to particle swarm optimisation, but particularly inspired by and based upon flies behaviour, and their tendency to swarm around a marker or point of interest. What differentiates this particular heuristic from it’s swarm intelligence parents is it’s characteristic to be disturbed; and consequently disperse at certain points in time, before re-swarming either to the same marker, or if a better one is found upon their displacement, a new point of interest (or optimum value).

As a result of this, it’s a more specific heuristic, I would estimate that the set of search/optimisation problems this could be useful for is fewer in comparison to a more general swarm optimisation (see wiki), but on this set of problems the performance will noticeably increase most of the time, a la No Free Lunch theorem (see my previous blog post here). A particular example where this may be useful is in Neural Network weight optimisation, (see my peer/friend Leon’s excellent post here for a practical example), when we use multi-layer perceptrons the search space becomes complex (resulting in local and global optima).

In computational ‘search’ problems, this is particularly useful as it allows complex search spaces with many ‘optimal’ solutions to be fully explored for both local optima and global optima. To clarify, let’s investigate the term search space.

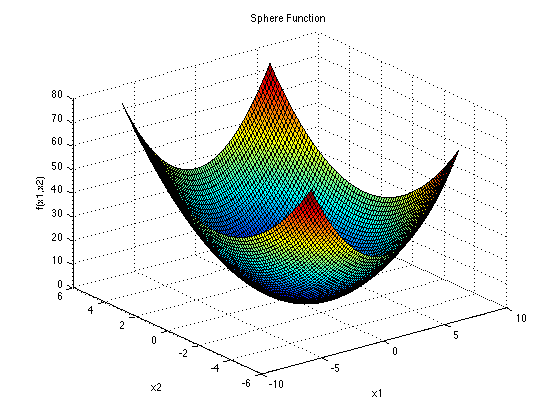
The most simple in 3-dimensions of search (or feature/data) space would be our parabola, or sphere function (search spaces can exist in any number of dimensions). Suppose in this instance x1 and x2 are our inputs, and the surface of the shape represents our output (or the set of all possible solutions), here the local minimum (optima) is the same as our global minimum. It can also be represented quite simply mathematically:

A nice example of a more complex search space is the ‘Hölder Table’ (which looks like waffle shaped table):

For more great looking (and also very practical ‘benchmarks’) test functions see the wiki here and more info with Matlab implementations here. (It is worth noting that it is very difficult to visualise anything above 3 dimensions!)

In DFO, first the population number (NP) of flies are initialised in random points in the feature space, according to a normal distribution. Then, the positions are updated taking three things into account, the current position, the position of the best neighbouring fly (which has the best fitness, to the left or right), and the position of the best fly (overall best fitness in the swarm). To determine the fitness, we have a ‘fitness function’ which is run once every iteration of the algorithm; the position of each fly in the feature space is evaluated against the other positions and then the ‘best’ fly is found according to its proximity to the optima (whether it is the minimum or maximum value, as defined by the problem space). The fitness function could be any mathematical function. For 2 dimensions we could simply say f(x1,x2) = (0,0) if we wanted to create a simple visualisation around a central point.

Now, to what makes this algorithm special, the dispersion threshold. To begin with we specify a value for the threshold, usually a small one! A random number (again using normal real distribution) between 0 and 1 is then generated and if the number falls below the dispersion threshold, the selected fly is assigned another random position, thus influencing it’s neighbours. This is a stochastic approach to making sure the swarm doesn’t focus on a local optima, and is forced to keep constantly searching around the space until the algorithm terminates (when the total number of evaluations is met), hopefully by then the global optima will have been found!*  This heuristic hopefully provides a balance between the key exploration and exploitation characteristics of swarm intelligence algorithms; our search is more diverse due to the dispersion and therefore we have more exploration, and we are stopping the swarm from exploiting specific areas too much.

I was wondering whether it would be an interesting approach for a recommendation system, due to the larger diversity of ‘best’ solutions (FF being highest rating) which would be found within a feature space. Particle Swarm Optimisation which is similar to DFO (minus the dispersion factor) has certainly been applied in this area successfully; notably here. Another interesting application is it’s use in medical imaging – utilising the intelligent agents (flies) to extend our cognitive abilities, in particular enhancing the visual perception of radiologists when detecting possible precancerous tissue.

To conclude my initial investigation, it seems there are many things to learn from nature and bringing an element of stochasticity can help us solve complex problems effectively. Swarm intelligence is a fascinating subset of AI; many minds are better than one when we are exploring a new field, and it’s always useful to visit new areas to avoid over exploiting just one solution to a complex problem.

Find the original DFO paper here.

 Applying It

I will now attempt to apply DFO to a well defined problem and something which has been of great interest to me recently; Recommendation Systems and in particular, Collaborative Filtering for music. Collaborative filtering is a very popular technique used within RS, the task is to find similar users to the current user based on their profiles, and make predictions which are appealing to the current user; ‘In the more general sense, collaborative filtering is the process of filtering for information or patterns using techniques involving collaboration among multiple agents, viewpoints, data sources, etc..’ [1]

I have been greatly inspired by work which applies Particle Swarm Optimisation to the task, most notably these papers on using PSO within CF; PSO RS, PSO for CF based on Fuzzy Features (for which my algorithm is mainly derived from) and for Swarm Intelligence in general applied to RS in Web Usage Mining.

Let’s define our model:

There are three phases needed to accomplish the recommendation task by using the DFO.

• User profile formation
• Neighbourhood set generation
• Predictions and recommendations

The user profile could be formed by a number of features: for this music application, I shall use the example of Discogs to inform the best features. For each release, we have the following; how many people have the item, how many people want the item, the average rating for the album (and each rating per user!) and Genres/Styles. There are numerous other features but I would argue that these are the most useful. We can develop new useful features like a Genre and Style ‘Interestingness Measure’ which can be represented more naturally by fuzzy sets (to fit better with average human perception), e.g very bad (VB), bad (B), average (AV), good (G), very good (VG), and excellent (E). When we then compute the similarities between users, we supposedly have more accurate results.

For the neighbourhood set generation; we need to find the optimum weights for every feature of our user profile — this takes into account the fact that different users place different priorities on features, for example user 1 might be mostly concerned with a genre while user 2 is mostly concerned with how highly an album is rated. for example which leads to the optimum feature space, where we have the most similar users. We could determine this by the RMSE of all the users euclidean distance (a quantitive measure of feature differences) to our current user, and perform DFO until we have the optimum solution. This would then lead to the most accurate recommendations (depending also on our process for selecting items from the users, e.g most commonly owned, highest rated etc.)

Now, for the Dispersive Flies optimisation! We have 4 main areas of concern; fly representation and initial population, the fitness function, fly behaviour and the termination condition.

Fly representation and initial population: we are mostly concerned with creating a vector (size dependent on population) of flies with parameters that represent their position, and thus the feature weights, in our n dimensional feature space.

The fitness function: This is very important. We need to evaluate the fitness score of each fly according to how well the weights map to our ideal ‘user space’ (the least RMSE distance of all users to our current user).

Fly behaviour: Each fly updates its position based on the best fly in the swarm, and it’s best neighbour. The dispersion threshold will be set to an initially small value, but this could be crucial to finding the best possible outcome in a finite amount of time when our data space is big (we could have thousands of users and millions of releases in those collections, and a high number of dimensions we will need to explore!)

 

t-SNE is a particularly useful way of visualising high dimensional data. Each point here could represent a different user

The success of this approach will be down to a number of performance measures, that compares the accuracy of the algorithm and the time it takes to reach the best user space. This is likely something that will become clearer to evaluate once we have run the algorithm a number of times, allowing adaptation of the parameters (dispersion threshold, number of flies). In our particular application, a little variance between different user spaces after each run of the algorithm could be useful in finding different recommendations.

This is not a completely detailed application and I will return to this after I have explored the problem further. There are a few other approaches within the field of recommendation that swarm intelligence could be particularly useful, particularly to solve the cold start problem; when we have a new user without many releases in their collection. Can we take more advantage of swarm optimisation for feature based recommendation?

Exploring new music can be a lot like finding new, unfamiliar territory, where the reward of finding something you like in a cluster of songs you don’t know can be extremely gratifying! Perhaps we can employ more inspiration from nature; ants are the some of the best explorers on our planet, could their meta-heuristics aid our search for new music? Tune in next time to find out.

Thanks for reading!

 

This is the second part in a series of  blogs for the Natural Computing module at Goldsmiths, University of London.

References:

[1] Terveen, Loren; Hill, Will (2001). “Beyond Recommender Systems: Helping People Help Each Other” (PDF). Addison-Wesley. p. 6.